Tous ces textes sont extraits de l’excellent site de vulgarisation de Physique Scio sur la physique quantique
Voir aussi l’excellent site « Etude de l’espace temps et de la gravitation » beaucoup plus technique.
La mécanique quantique est à présent, elle et les théories qui en sont issues, comme la théorie quantique des champs, la théorie la mieux vérifiée expérimentalement. On a beaucoup dit qu’elle était la théorie la plus éloignée de notre logique.
La mécanique quantique, la théorie, la vraie, ne fournit que des outils mathématiques très complexes qui permettent de prévoir les résultats des mesures. Elle dit « voici ce que vous allez mesurer ». Elle ne dit pas « voici ce qui s’est passé ». Et pour cause ! Tout ce qui se passe en mécanique quantique n’est pas accessible à notre expérience directe : on ne peut pas constater de nos yeux ce qui se passe. Tout est donc une question d’interprétation, et pour l’instant il en existe plusieurs qui ne sont pas départagées, parce qu’elles expliquent toutes, bien que d’une manière différente, pourquoi on observe ce qu’on observe.
Ce qui est présenté ici est une interprétation plutôt moderne, on va dire. Et peut-être qu’on pourra un jour départager toutes ces interprétations. Mais peut-être que ça n’est pas la bonne. Il faut prendre tout ça avec prudence…
1. Comment imaginer une particule de matière ?
Longtemps on a pensé que les particules qui nous composaient étaient des sortes de petites billes dures. On a donc imaginé par exemple que les atomes étaient comme des systèmes planétaires, où des électrons tournaient autour du noyau comme les planètes tournent autour du soleil. Mais on a fait des expériences qu’on ne pouvait pas expliquer si on continuait de considérer que les particules étaient « ponctuelles », c’est à dire des petites billes dures. Ce sont les premiers résultats de la mécanique quantique. Un électron par exemple c’est tout le contraire d’une bille indéformable : c’est au contraire un « blob », un nuage léger et très déformable. En général, on trouve les électrons dans les atomes : ils forment ce qu’on appelle le « nuage électronique », c’est à dire un nuage d’électrons autour d’un noyau qui lui ressemble, vu de loin, à une petite sphère indéformable.
|
|
|
|
Ondulatoire |
Corpusculaire |
Deux électrons peuvent se marcher sur les pieds, c’est à dire s’interpénétrer. Par contre, ils ne peuvent absolument pas se « recouvrir » complètement : c’est ce qu’on appelle « le principe d’exclusion ». Il est en fait le signe de quelque chose de beaucoup plus profond qu’on aborde dans la théorie fille de la mécanique quantique, la théorie des champs.
Un électron est donc un petit nuage. Ce nuage peut parfaitement se diviser en deux, avec chacun des morceaux allant dans une direction différente, pourquoi pas. Mais vous voyez du coup qu’il n’est plus possible de dire où est l’électron, ni quelle est sa vitesse. Puisque l’électron n’est pas une bille, ces questions n’ont aucun sens.
Imaginez maintenant que ces deux morceaux d’électrons s’éloignent l’un de l’autre : cela reste cependant la même particule. Un exemple ? Eh bien en appuyant sur un des morceaux, l’autre réagit instantanément. C’est normal, puisque c’est la même particule ! Cela s’appelle la « non-localité ».
En général, et c’est important, les électrons n’occupent guère plus de place qu’un atome. Il est rare qu’il leur soit donné la possibilité de prendre leurs aises, et de s’étaler. Mais lorsqu’ils le font, on s’aperçoit qu’ils se comportent comme des ondes : prenons encore nos deux morceaux d’un même électron, et imaginons qu’ils se rencontrent. Eh bien le résultat n’est pas simplement l’addition des deux morceaux : il se produit ce qu’on appelle des interférences, ce qui est une propriété que l’on croyait réservée aux ondes !

La lumière est justement composée de particules, appelées photons. Chacune de ces particules est capable d’interférer avec elle-même, et de produire donc des interférences. Donc un troupeau de ces particules produit des interférences, puisqu’elles le font toutes. Ce qui explique que la lumière se comporte comme une onde : elle fait des interférences. Et on a mis longtemps à comprendre que la lumière n’était pas seulement une onde, mais bien constituée de particules.
 |
Aidons-nous de l’analogie suivante:Regardé sous deux angles différents, un cylindre nous apparaît tantôt comme un cercle, tantôt comme un rectangle. Pourtant il n’est ni l’un ni l’autre.Ainsi en est-il du photon, de l’électron ou de toute particule élémentaire dont l’image corpusculaire ne serait qu’une facette d’une entité plus complexe.Ce point précis peut poser un problème philosophique très troublant: La réalité objective (s’il elle existe indépendamment de l’esprit humain) est-elle accessible ? Ou sommes-nous condamner à n’observer qu’un monde d’apparences trompeuses? |
Ce sont les premières leçons que vous donne la mécanique quantique : les particules de matière sont parfaitement « déformables », ce ne sont pas des billes minuscules, et du coup, elles sont capables de se comporter comme des ondes. Mais que l’on agisse sur une partie de la particule, et instantanément, le reste réagit.
2. La quantification de l’infiniment petit.
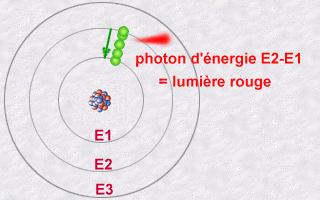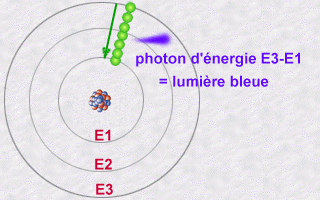
En regardant la lumière qu’émettaient les atomes, on s’est aperçu qu’un atome d’un élément donné (comme le carbone, ou l’hydrogène) n’émettait que des couleurs très précises, ce qu’on appelle un spectre de raies.
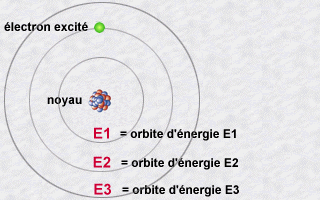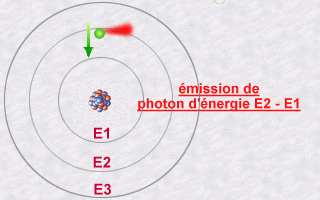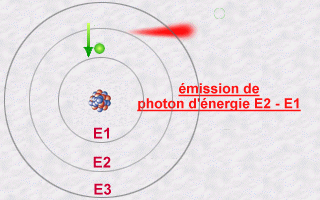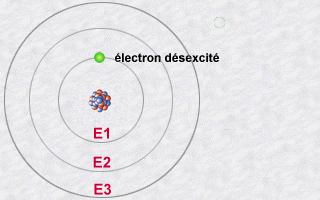
On a imaginé au début qu’en fait les électrons étaient des petites billes qui tournaient autour du noyau, et que le fait que les atomes n’émettent qu’un certain type de lumière signifiait que seules certaines orbites étaient permises, c’est à dire que les électrons ne pouvaient pas tourner à la distance qu’ils voulaient, mais à des distances fixées du noyau. On pensait que la lumière émise était le signe d’un changement d’orbite. Ce n’est pas vraiment ça, puisqu’un électron n’est pas une petite bille…
On a donc fini par comprendre que c’était dû aux changements de forme de l’électron autour de l’atome. Quand on observe un atome, c’est à dire qu’on cherche à savoir comment sont les électrons qui entourent le noyau, on trouve toujours que les électrons adoptent des formes particulières. On a continué à les appeller des orbitales atomiques, comme quand on croyait que l’électron était une bille, juste pour ne pas changer.
 |
 |
 |
En fait, on en a déduit (parce qu’on ne peut pas vraiment voir les orbitales, c’est à dire les formes des électrons), que les électrons ne bougeaient pas autour des noyaux, ils prenaient simplement des formes particulières. La plus simple, c’est juste une sphère autour du noyau, mais il en existe plein, et des compliquées…
C’est ça, la quantification : le fait que ce qu’on croyait « continu » était « discret ». Par exemple qu’on ne voit pour les électrons que des formes précises, et pas n’importe quelle forme. C’est pour cela qu’on a appelé la mécanique de l’infiniment petit la mécanique quantique : parce que dans l’infiniment petit, le discret intervient bien plus souvent que le continu.
Par exemple, on pensait aussi que la lumière était « continue », qu’on pouvait en émettre aussi peu qu’on voulait. En fait, on s’est aperçu que la lumière aussi pouvait être quantifiée : on n’envoie toujours un certain nombre de « grains » de lumière, ce qu’on appelle des quanta (pluriel de un quantum). On a appelé le quantum de lumière, donc la particule, un photon. Et on ne peut pas envoyer moins de lumière qu’un photon !
3. La « propriété » de superposition
En réalité, un électron autour d’un noyau atomique peut prendre absolument n’importe quelle forme, rien ne l’en empêche. Mais alors, est-ce que je viens de dire n’importe quoi ? Non, pas du tout. Je vous ai bien dit que lorsqu’on cherchait à savoir quelle forme l’électron avait autour du noyau, on trouvait des formes particulières appelées orbitales. Mais c’était seulement le résultat des mesures.
En fait, l’électron est un grand timide : dès lors qu’on cherche à savoir comme il est, il se réfugie sur une orbitale, c’est à dire qu’il prend une forme particulière. Les états quelconques de l’électron sont particulièrement fragiles. L’interaction de l’atome (et de l’électron) avec un instrument de mesure le perturbe forcément (songez que nos appareils de mesure sont constitués de milliards de milliards de particules), et les formes quelconques de l’atome autour du noyau sont particulièrement fragiles : l’interaction avec l’appareil de mesure les détruit et l’électron prend alors une forme « résistante », c’est à dire une orbitale.
La question qu’on pourrait se poser, c’est alors : et si on imagine qu’on connaît l’état initial de l’électron, sa forme quelconque, est-ce qu’on peut prévoir ce qu’on va obtenir comme orbitale après la mesure ? Eh bien oui, et on va voir comment.
Si vous prenez l’électron dans sa forme quelconque, on peut toujours décomposer cette forme en orbitales : c’est à dire qu’on peut dire « Ah, cette forme, c’est comme si l’électron était à 30% sur cette orbitale ci et à 70% sur cette orbitale là ». Ca n’est qu’une façon de voir, en fait, puisque l’électron a une forme bien déterminée, mais indépendante des formes particulières que sont les orbitales.
Par contre, cette façon de voir prend toute son importance au moment où on cherche à connaître la forme de l’électron, c’est à dire où on fait une mesure. On ne contrôle pas à ce moment là ce qui se passe (l’instrument de mesure est trop gros pour qu’on sache exactement quelle va être son influence sur l’électron), mais on sait que plus une orbitale était dans la forme de l’électron, plus elle a de chance d’être choisie comme « refuge » par l’électron. Donc, pour le cas que nous considérons, après la mesure, l’électron a 30% de chances de se retrouver sur une orbitale et 70% sur une autre !
Avant la mesure, l’électron avait bien une forme à lui et cette forme permettait de prédire quelles étaient les chances de chaque résultat. Après la mesure, l’électron est sur une orbitale précise, c’est à dire qu’il a une forme bien connue.
On peut décomposer n’importe quelle forme en orbitales (avec un certain pourcentage pour chaque orbitale), et l’électron en général avant la mesure n’est pas sur une orbitale. On dit qu’il a un état superposé : il est en quelque sorte sur plusieurs orbitales à la fois (ce qui peut paraître paradoxal, si on ne sait pas que cela correspond simplement à une forme différente d’une orbitale précise).
Dans le cas précédent, on a étudié ce qui arrivait à un électron qui ne peut pas échapper à l’attraction du noyau atomique. On va regarder maintenant ce qui arrive à un électron « libre », c’est à dire qui n’est attaché à aucun atome.
Laissé à lui-même, un électron libre peut prendre ses aises, et s’étaler jusqu’à atteindre des tailles de quelques millimètres ! Ce qui est énorme pour un électron. C’est des millions de fois plus gros qu’un atome. Mais on n’a que des preuves indirectes du fait qu’un électron libre est capable d’atteindre cette taille.
En effet, pour savoir où il est, il faut le faire interagir avec, par exemple un écran qui produit de la lumière là où l’électron arrive. Mais ce qu’on observe, ça n’est jamais une tache de quelques millimètres, mais un point de quelques micromètres au plus.
C’est à dire que l’électron n’interagit qu’avec une petite partie de l’écran, quoi qu’il arrive ! C’est pour cela qu’on a mis si longtemps à admettre que l’électron n’était pas une bille : on voyait toujours un point sur l’écran.
En fait, ce qui se passe est simple, cela ressemble à ce qui se passe avec les orbitales atomiques : lorsque l’électron interagit avec l’écran, il est perturbé, et il se rétracte très rapidement pour redevenir petit (disons de la taille de ses congénères dans les atomes – donc de la taille d’un atome, quoi). Lorsque l’électron s’étale, son état est fragile et le moindre contact avec un objet assez gros suffit à le faire se rétracter. Un électron « coup » en deux » est un électron étalé. Prenons un électron coupé en deux avec 45% de son nuage groupé d’un côté, et 55% de l’autre. Au moment où l’électron interagit avec l’écran, ce contact fait fondre immédiatement l’un des deux morceaux, et c’est le morceau restant qui produit la lumière sur l’écran. Un électron étalé est instable, et la moindre perturbation suffit à lui faire quitter cet état.
Plus l’électron est présent en un endroit, plus il a de chances que le contact avec l’écran le fasse se condenser complètement en cet endroit. Si l’électron était situé à 55% en un endroit, il a 55% d’y apparaître entièrement lors de la mesure, c’est à dire du contact avec l’écran !
On peut donc dire là aussi que l’électron était dans deux états superposés : ici et là-bas. Si on considère que l’électron est une bille, cela paraît exceptionnel – mais si vous considérez que l’électron est un nuage, un blob, cela n’a rien d’exceptionnel. C’est juste une façon de voir…
5. Corrélation et décohérence.
Prenons deux particules quelconques, par exemple des électrons. Si on fait interagir ces deux particules (on les fait se cogner, par exemple, on les rapproche), elles peuvent se corréler plus ou moins.
Cela signifie que l’état de la particule A dépendra étroitement de l’état de la particule B. Et si vous perturbez la particule A, B sera instantanément perturbée, quelque soit la distance qui les séparait.
Si le changement qui intervient sur B est grand, c’est que les particules étaient très corrélées. S’il est faible, c’est que les particules étaient faiblement corrélées. C’est une propriété assez folle non ? Un peu comme si les particules étaient capables de télépathie…

Il faut cependant savoir que, de la même manière que ce qu’on appelle les états superposés, les états corrélés sont très fragiles. Si vous prenez A et B, le contact de A avec un objet assez gros (un gros paquet d’atomes) va forcément détruire la corrélation entre A et B. Ca perturbe bien évidemment B au passage, puisqu’on touche à A, mais ensuite, A et B feront comme s’ils ne s’étaient jamais rencontrés. La corrélation sera détruite.
Un exemple ? Comment sait-on qu’un électron a changé d’orbitale ? Quand il envoie un photon. Seulement, en fait, un électron n’est pas nécessairement sur une orbitale. Le photon qu’il envoie est corrélé avec l’électron qui a changé de forme. En détectant le photon, c’est là qu’on va projeter l’électron sur une orbitale : en fait, de mesurer les propriétés du photon agit directement sur l’électron et le fait se réfugier sur une orbitale.
Ainsi est la mécanique quantique : on est obligé de deviner les états dans lesquels peuvent se trouver les particules, parce que les mesures ne peuvent pas nous les montrer. Car lorsqu’on mesure, on détruit forcément ces états si particuliers, comme les formes quelconques d’un électron autour d’un noyau, ou encore les électrons libres « étalés » dans l’espaces ou les particules corrélées. L’interaction de particules dans ces états fragiles avec un paquet d’atome suffit à les détruire : c’est ce qu’on appelle la décohérence.
Et vous voyez à présent combien il a été difficile de comprendre ce qui se passait simplement à partir des résultats des mesures…
Pour ceux qui n’ont pas tout compris :







vidéo super au top ! à lire le livre des hators
bah voilà ! quand vous voulez vous pouvez faire autre chose que du bullshit pute à clic.
sincères félicitations, continuez comme ça.
l’important c’est pas uniquement ce qu’on peut faire, c’est aussi ce que toi tu peux faire 😉
envois nous tes articles qu’on les publie.